Predict Underlying

1. Imports

import torch
import matplotlib.pyplot as plt 

2. 회귀분석

- 목적은 아래와 같이 데이터들에 잘 맞는 회귀선을 찾는 것

torch.manual_seed(21345)
ones= torch.ones(100).reshape(-1,1)
x,_ = torch.randn(100).sort()
x = x.reshape(-1,1)
X = torch.concat([ones,x],axis=-1)
W = torch.tensor([[2.5],[4]])
ϵ = torch.randn(100).reshape(-1,1)*0.5
y = X@W + ϵ

plt.plot(x,y,'o')
plt.plot(x,2.5+4*x,'--')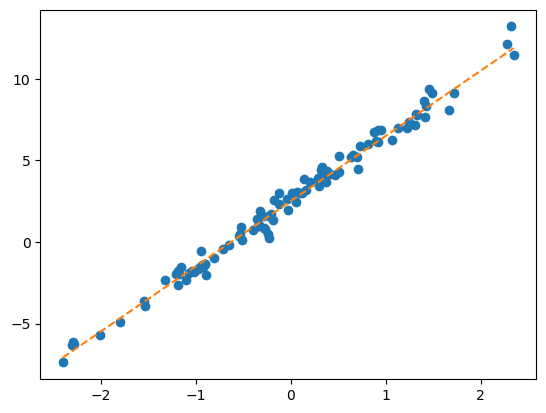

- 회귀모형에서 학습이란 위의 그림처럼 주황색 점선을 더 정확하게 추정하는 것

3. 학습

임의의 W값을 생각하자 그 다음 더 좋은 W값을 찾아서 업데이트 하면 되지 않을까?

- Step1: Data

데이터를 torch.tensor의 2차원 배열로 바꿔준다 .reshape(-1,1)을 사용 <- 행렬계산을 해야하기에 2차원배열로 바꾸는 것

- Step2: Update

업데이트를 할 건데 뭘 어떻게 좋게 만들 것인지 기준을 잡아야한다. -> Loss!(SSE)

회귀직선이 정확할 수록 Loss가 작다.

그렇다면 Loss값을 가장 작게 하는 W를 어떻게 찾을까?

Step2-1: update의 정도를 파악하고 수정하는 과정

1. 임의의 점 \(\hat{w}\) 를 찍는다.

2. 2.loss(W)의 기울기를 계산

3. \(\hat{w}\) - \(\alpha\) \(\frac{d}{dW}loss(W)\)

Step2-2: \(\hat{w}\) 수정

Wbefore = What.data

Wafter = What.data - \(\alpha\) * What.grad

- Step3: 미분

loss.backward()를 사용하면 What.grad()에 값이 생긴다. 곧 미분값

- Step4: iteration

for문을 사용하여 반복학습 해준다

4. 각 Step의 변형

- Step2의 변형

MSELoss()를 이용한다.

- Step1의 변형

net오브젝트를 이용하여 원활한 학습을 위한 데이터 정리를 해준다.

- Step4의 변형

optimizer 오브젝트를 이용하여 학습을 진행한다.

temp = [-2.4821, -2.3621, -1.9973, -1.6239, -1.4792, -1.4635, -1.4509, -1.4435,
        -1.3722, -1.3079, -1.1904, -1.1092, -1.1054, -1.0875, -0.9469, -0.9319,
        -0.8643, -0.7858, -0.7549, -0.7421, -0.6948, -0.6103, -0.5830, -0.5621,
        -0.5506, -0.5058, -0.4806, -0.4738, -0.4710, -0.4676, -0.3874, -0.3719,
        -0.3688, -0.3159, -0.2775, -0.2772, -0.2734, -0.2721, -0.2668, -0.2155,
        -0.2000, -0.1816, -0.1708, -0.1565, -0.1448, -0.1361, -0.1057, -0.0603,
        -0.0559, -0.0214,  0.0655,  0.0684,  0.1195,  0.1420,  0.1521,  0.1568,
         0.2646,  0.2656,  0.3157,  0.3220,  0.3461,  0.3984,  0.4190,  0.5443,
         0.5579,  0.5913,  0.6148,  0.6469,  0.6469,  0.6523,  0.6674,  0.7059,
         0.7141,  0.7822,  0.8154,  0.8668,  0.9291,  0.9804,  0.9853,  0.9941,
         1.0376,  1.0393,  1.0697,  1.1024,  1.1126,  1.1532,  1.2289,  1.3403,
         1.3494,  1.4279,  1.4994,  1.5031,  1.5437,  1.6789,  2.0832,  2.2444,
         2.3935,  2.6056,  2.6057,  2.6632]
sales= [-8.5420, -6.5767, -5.9496, -4.4794, -4.2516, -3.1326, -4.0239, -4.1862,
        -3.3403, -2.2027, -2.0262, -2.5619, -1.3353, -2.0466, -0.4664, -1.3513,
        -1.6472, -0.1089, -0.3071, -0.6299, -0.0438,  0.4163,  0.4166, -0.0943,
         0.2662,  0.4591,  0.8905,  0.8998,  0.6314,  1.3845,  0.8085,  1.2594,
         1.1211,  1.9232,  1.0619,  1.3552,  2.1161,  1.1437,  1.6245,  1.7639,
         1.6022,  1.7465,  0.9830,  1.7824,  2.1116,  2.8621,  2.1165,  1.5226,
         2.5572,  2.8361,  3.3956,  2.0679,  2.8140,  3.4852,  3.6059,  2.5966,
         2.8854,  3.9173,  3.6527,  4.1029,  4.3125,  3.4026,  3.2180,  4.5686,
         4.3772,  4.3075,  4.4895,  4.4827,  5.3170,  5.4987,  5.4632,  6.0328,
         5.2842,  5.0539,  5.4538,  6.0337,  5.7250,  5.7587,  6.2020,  6.5992,
         6.4621,  6.5140,  6.6846,  7.3497,  8.0909,  7.0794,  6.8667,  7.4229,
         7.2544,  7.1967,  9.5006,  9.0339,  7.4887,  9.0759, 11.0946, 10.3260,
        12.2665, 13.0983, 12.5468, 13.8340]

x = torch.tensor(temp).reshape(-1,1)
ones = torch.ones(100).reshape(-1,1)
X = torch.concat([ones,x],axis=1)
y = torch.tensor(sales).reshape(-1,1)

net = torch.nn.Linear(
    in_features=2,
    out_features=1,
    bias=False
)
net.weight.data = torch.tensor([[-5.0,  10.0]])

loss_fn = torch.nn.MSELoss()

optimizr = torch.optim.SGD(net.parameters(),lr=0.1)
for epoc in range(30):
    # step1: yhat 
    yhat = net(X)
    # step2: loss
    loss = loss_fn(yhat,y)
    # step3: 미분
    loss.backward()
    # step4: update
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'o')
plt.plot(x,yhat.data,'--')
plt.title(f'net.weight={net.weight.data.reshape(-1)}');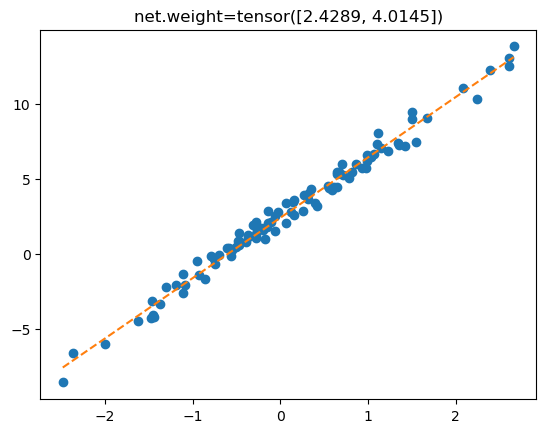

5. 로지스틱

x = torch.tensor([-6,-5,-4,-3,-2,-1, 0, 1, 2, 3, 4, 5, 6.0]).reshape(-1,1)
y = torch.tensor([ 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1]).reshape(-1,1)
plt.plot(x,y,'o')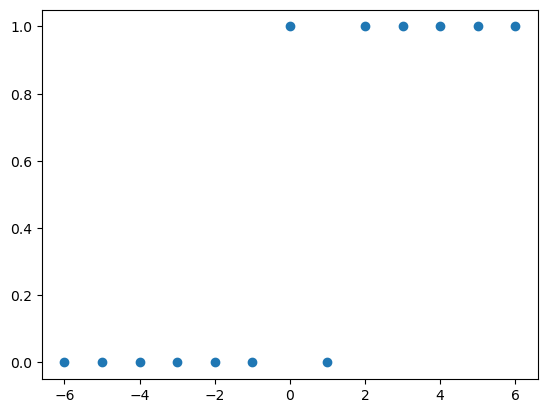

- 위와 같은 범주형 문제는 이전의 문제처럼 회귀문제로 생각하는 건 쉽지 않아 보인다. 로지스틱으로 해볼까?

우리가 예측하고 싶은 건 underlying이다.

x = torch.linspace(-1,1,2000).reshape(2000,1)
w0 = -1
w1 = 5
u = w0 + x*w1 
v = torch.exp(u) / (1+torch.exp(u)) # logistic
y = torch.bernoulli(v) # 베르누이

net = torch.nn.Sequential(
    torch.nn.Linear(in_features=1, out_features=1),
    torch.nn.Sigmoid()
)
l1, a1 = net
l1.weight.data = torch.tensor([[-0.3]])
l1.bias.data = torch.tensor([-0.8])
optimizr = torch.optim.SGD(net.parameters(),lr=0.25)
#---#
for epoc in range(100):
    ## 1
    yhat = net(x) 
    ## 2 
    loss = torch.mean((y-yhat)**2)
    ## 3
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'.',alpha=0.05)
plt.plot(x,v,'--r')
plt.plot(x,yhat.data,'--b')
plt.title('after 100 epochs')

Text(0.5, 1.0, 'after 100 epochs')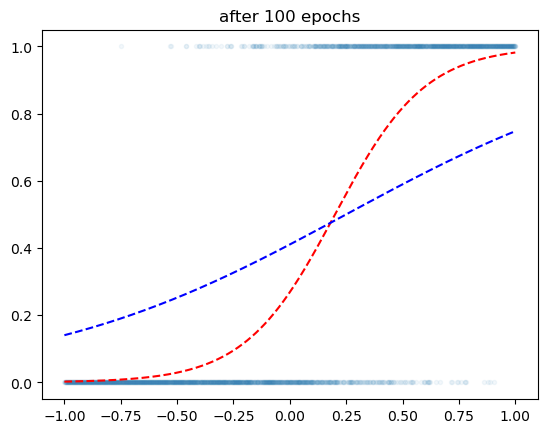

5000번 학습하면?

x = torch.linspace(-1,1,2000).reshape(2000,1)
w0 = -1
w1 = 5
u = w0 + x*w1 
v = torch.exp(u) / (1+torch.exp(u)) # logistic
y = torch.bernoulli(v) # 베르누이

net = torch.nn.Sequential(
    torch.nn.Linear(in_features=1, out_features=1),
    torch.nn.Sigmoid()
)
l1, a1 = net
l1.weight.data = torch.tensor([[-0.3]])
l1.bias.data = torch.tensor([-0.8])
optimizr = torch.optim.SGD(net.parameters(),lr=0.25)
#---#
for epoc in range(5000):
    ## 1
    yhat = net(x) 
    ## 2 
    loss = torch.mean((y-yhat)**2)
    ## 3
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'.',alpha=0.05)
plt.plot(x,v,'--r')
plt.plot(x,yhat.data,'--b')
plt.title('after 100 epochs')

Text(0.5, 1.0, 'after 100 epochs')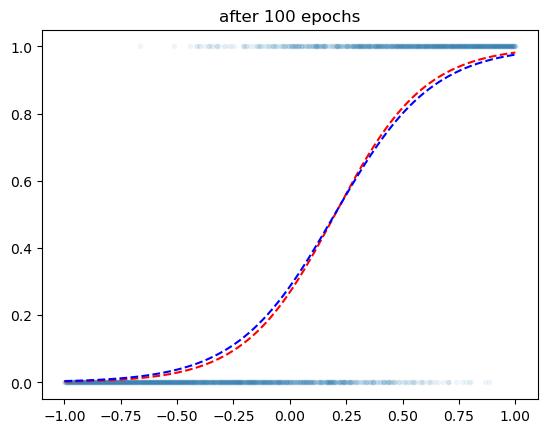

6. 초기값의 중요성

import torch
import matplotlib.pyplot as plt 
import numpy as np
import pandas as pd

def plot_loss(loss_fn, ax=None, Wstar=[-1,5]):
    w0hat,w1hat =torch.meshgrid(torch.arange(-10,3,0.1),torch.arange(-1,10,0.1),indexing='ij')
    w0hat = w0hat.reshape(-1)
    w1hat = w1hat.reshape(-1)
    def l(w0hat,w1hat):
        yhat = torch.exp(w0hat+w1hat*x)/(1+torch.exp(w0hat+w1hat*x))
        return loss_fn(yhat,y) 
    loss = list(map(l,w0hat,w1hat))
    #---#
    if ax is None: 
        fig = plt.figure()
        ax = fig.add_subplot(1,1,1,projection='3d')
    ax.scatter(w0hat,w1hat,loss,s=0.001) 
    ax.scatter(w0hat[::20],w1hat[::20],loss[::20],s=0.1,color='C0') 
    w0star,w1star = np.array(Wstar).reshape(-1)
    ax.scatter(w0star,w1star,l(w0star,w1star),s=200,marker='*',color='red',label=f"W=[{w0star:.1f},{w1star:.1f}]")
    #---#
    ax.elev = 15
    ax.dist = -20
    ax.azim = 75    
    ax.legend()
    ax.set_xlabel(r'$w_0$')  # x축 레이블 설정
    ax.set_ylabel(r'$w_1$')  # y축 레이블 설정
    ax.set_xticks([-10,-5,0])  # x축 틱 간격 설정
    ax.set_yticks([-10,0,10])  # y축 틱 간격 설정

def learn_and_record(net, loss_fn, optimizr):
    yhat_history = [] 
    loss_history = []
    What_history = []
    Whatgrad_history = []
    What_history.append([net[0].bias.data.item(), net[0].weight.data.item()])
    for epoc in range(100): 
        ## step1 
        yhat = net(x)
        ## step2 
        loss = loss_fn(yhat,y)
        ## step3
        loss.backward() 
        ## step4 
        optimizr.step()
        ## record 
        if epoc % 5 ==0: 
            yhat_history.append(yhat.reshape(-1).data.tolist())
            loss_history.append(loss.item())
            What_history.append([net[0].bias.data.item(), net[0].weight.data.item()])
            Whatgrad_history.append([net[0].bias.grad.item(), net[0].weight.grad.item()])
        optimizr.zero_grad() 
        
    return yhat_history, loss_history, What_history, Whatgrad_history

def show_animation(net, loss_fn, optimizr):
    yhat_history,loss_history,What_history,Whatgrad_history = learn_and_record(net,loss_fn,optimizr)
    
    fig = plt.figure(figsize=(7.5,3.5))
    ax1 = fig.add_subplot(1, 2, 1)
    ax2 = fig.add_subplot(1, 2, 2, projection='3d')
    ## ax1: 왼쪽그림 
    ax1.scatter(x,y,alpha=0.01)
    ax1.scatter(x[0],y[0],color='C0',label=r"observed data = $(x_i,y_i)$")
    ax1.plot(x,v,'--',label=r"prob (true) = $(x_i,\frac{exp(-1+5x_i)}{1+exp(-1+5x_i)})$")    
    line, = ax1.plot(x,yhat_history[0],'--',label=r"prob (estimated) = $(x_i,\hat{y}_i)$") 
    ax1.legend()
    ## ax2: 오른쪽그림 
    plot_loss(loss_fn,ax2)
    ax2.scatter(np.array(What_history)[0,0],np.array(What_history)[0,1],loss_history[0],color='blue',s=200,marker='*')    
    def animate(epoc):
        line.set_ydata(yhat_history[epoc])
        w0hat = np.array(What_history)[epoc,0]
        w1hat = np.array(What_history)[epoc,1]
        w0hatgrad = np.array(Whatgrad_history)[epoc,0]
        w1hatgrad = np.array(Whatgrad_history)[epoc,1]
        ax2.scatter(w0hat,w1hat,loss_history[epoc],color='grey')
        ax2.set_title(f"What.grad=[{w0hatgrad:.4f},{w1hatgrad:.4f}]",y=0.8)
        fig.suptitle(f"epoch={epoc*5} // What=[{w0hat:.2f},{w1hat:.2f}] // Loss={loss_fn.__class__.__name__} // Opt={optimizr.__class__.__name__}")
        return line
    ani = animation.FuncAnimation(fig, animate, frames=20)    
    plt.close()
    return ani

- 좋은 초기값

from matplotlib import animation
plt.rcParams["animation.html"] = "jshtml"

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-0.8])
net[0].weight.data = torch.tensor([[-0.3]])
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.25) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

- 최악의 초기값

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-10.0])
net[0].weight.data = torch.tensor([[-1.0]])
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.25) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

7. 손실함수의 개선

Loss 중 BCELoss라는 것이 있는데 이것은 반복을 했을 때 원하는 만큼 움직이지 않는다면 가속도를 붙혀서 그 다음 반복시에는 더 많이 움직이게끔 방식이다.

여기서 움직이게 한다는 건 Loss를 줄여서 적합을 시킨다는 의미이다.

사용방법은 loss를 선언할 때 BCELoss() 라고 쓰면 된다

net = torch.nn.Sequential(
    torch.nn.Linear(in_features=1, out_features=1),
    torch.nn.Sigmoid()
)
l1, a1 = net # 네트워크는 섭스크립터블 오브젝트이니까..
l1.weight.data = torch.tensor([[-0.3]])
l1.bias.data = torch.tensor([-0.8])
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.25)
#---#
for epoc in range(100):
    ## 1
    yhat = net(x) 
    ## 2 
    loss = loss_fn(yhat,y) # yhat부터 써야함
    ## 3
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'.',alpha=0.05)
plt.plot(x,v,'--r')
plt.plot(x,yhat.data,'--b')
plt.title('after 100 epochs')

Text(0.5, 1.0, 'after 100 epochs')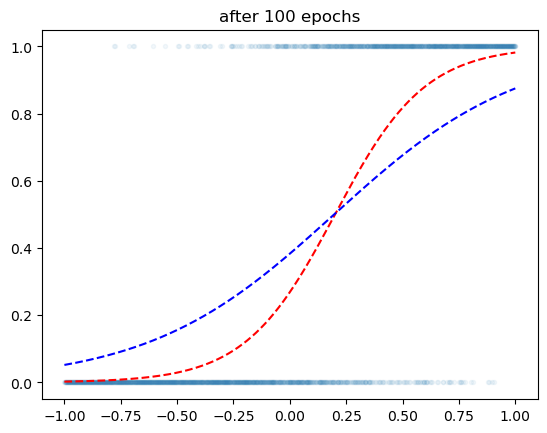

- MSELoss를 사용할 때보다 BCELoss를 사용했을 때 훨씬 더 적합이 되는 듯한 느낌이다.

fig = plt.figure()
ax1 = fig.add_subplot(1,2,1,projection='3d')
ax2 = fig.add_subplot(1,2,2,projection='3d')
plot_loss(torch.nn.MSELoss(),ax1)
plot_loss(torch.nn.BCELoss(),ax2)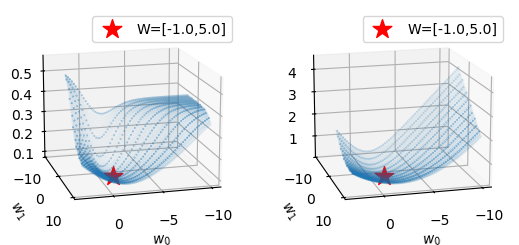

뭔가 더 잘 떨어지게끔 오른쪽이 미끄럼틀같이 펴져있다.

- MSELoss

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-0.8])
net[0].weight.data = torch.tensor([[-0.3]])
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.25) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

- BCELoss

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-0.8])
net[0].weight.data = torch.tensor([[-0.3]])
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.25) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

8. 옵티마이저의 개선

- MSELoss + SGD

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-10.0])
net[0].weight.data = torch.tensor([[-1.0]])
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.SGD(net.parameters(),lr=0.05) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

꿈쩍도 하지 않는 모습…

- MSELoss + Adam

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
) 
net[0].bias.data = torch.tensor([-10.0])
net[0].weight.data = torch.tensor([[-1.0]])
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters(),lr=0.25) 
#---#
show_animation(net,loss_fn,optimizr)

Once Loop Reflect

너무나도 뚝뚝 잘 내려온다

- 그럼 BCELoss + Adam 쓰면 무적인가?

9.로지스틱의 한계

df = pd.read_csv("https://raw.githubusercontent.com/guebin/DL2024/main/posts/dnnex.csv")
x = torch.tensor(df.x).float().reshape(-1,1)
y = torch.tensor(df.y).float().reshape(-1,1)
prob = torch.tensor(df.prob).float().reshape(-1,1)
plt.plot(x,y,'o',alpha=0.02)
plt.plot(x[0],y[0],'o',label= r"observed data = $(x_i,y_i)$",color="C0")
plt.plot(x,prob,'--b',label= r"prob (true, unknown)")
plt.legend()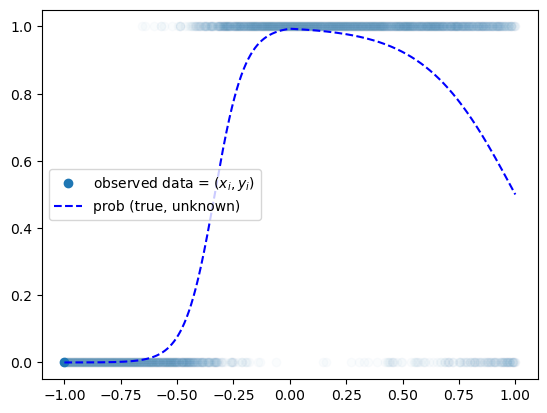

- 이런 꺾인 선은 로지스틱으로 적합하기 힘들어…

net = torch.nn.Sequential(
    torch.nn.Linear(1,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
#---# 
for epoc in range(5000):
    ## 1 
    yhat = net(x)
    ## 2 
    loss = loss_fn(yhat,y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'o',alpha=0.02)
plt.plot(x[0],y[0],'o',label= r"observed data = $(x_i,y_i)$",color="C0")
plt.plot(x,prob,'--b',label= r"prob (true, unknown)")
plt.plot(x,net(x).data, '--', label= r"prob (estimated) = $(x_i,\hat{y}_i)$")
plt.legend()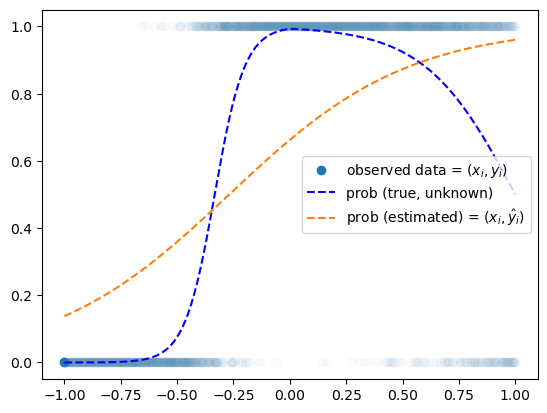

10.로지스틱의 한계 극복

ReLU : 음수인 것은 0으로 만들고 양수는 그대로 둔다. 그럼 그래프가 꺾인다.

y = x*0 
y[x<0] = (9*x+4.5)[x<0]
y[x>0] = (-4.5*x+4.5)[x>0]

plt.plot(y,'--')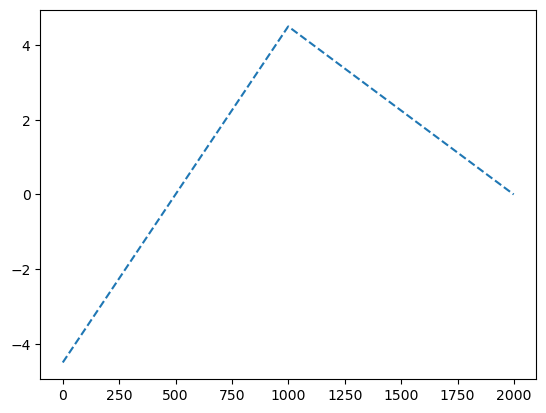

df = pd.read_csv("https://raw.githubusercontent.com/guebin/DL2024/main/posts/dnnex.csv")
x = torch.tensor(df.x).float().reshape(-1,1)
y = torch.tensor(df.y).float().reshape(-1,1)
prob = torch.tensor(df.prob).float().reshape(-1,1)

torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(1,2),
    torch.nn.ReLU(),
    torch.nn.Linear(2,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
#---#
for epoc in range(3000):
    ## 
    yhat = net(x)
    ## 
    loss = loss_fn(yhat,y)
    ## 
    loss.backward()
    ## 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'o',alpha=0.02)
plt.plot(x[0],y[0],'o',label= r"observed data = $(x_i,y_i)$",color="C0")
plt.plot(x,prob,'--b',label= r"prob (true, unknown)")
plt.plot(x,net(x).data,'--',label="prob (estimated) -- after 3000 epochs")
plt.legend()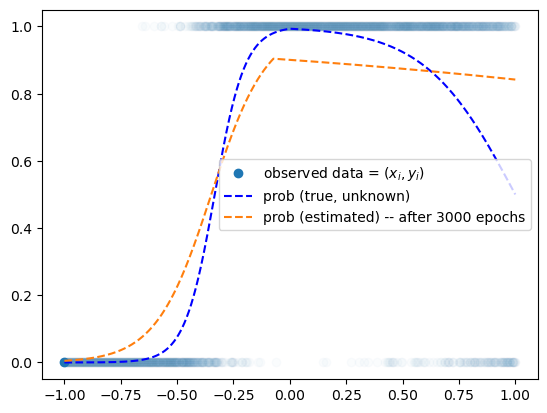

for epoc in range(3000):
    ## 
    yhat = net(x)
    ## 
    loss = loss_fn(yhat,y)
    ## 
    loss.backward()
    ## 
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,'o',alpha=0.02)
plt.plot(x[0],y[0],'o',label= r"observed data = $(x_i,y_i)$",color="C0")
plt.plot(x,prob,'--b',label= r"prob (true, unknown)")
plt.plot(x,net(x).data,'--',label="prob (estimated) -- after 6000 epochs")
plt.legend()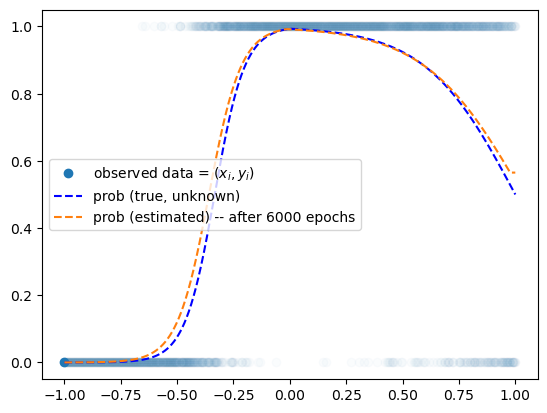

ReLU에 대해서는 깊게 알기보단 그래프를 꺾을 수 있다

그 꺾는다는 의미는 표현력을 높인다고 생각하는 것이 좋다.

로지스틱의 한계를 마주했을 때 그저 증가함수는 표현을 못 하는 그래프들이 있기때문에 문제였는데

이제 ReLU를 이용해서 꺾인 선 그래프도 그릴 수 있게 되었고 그것으로 적합해서 맞춰나가면 해결할 수 있게 되었다.

즉 그래프의 표현력이 늘었다. 그렇다면 모든 그래프도 적합할 수 있을 거 같은데?

torch.manual_seed(21345)
x = torch.linspace(0,2,2000).reshape(-1,1)
eps = torch.randn(2000).reshape(-1,1)*0.05
fx = torch.exp(-1*x)* torch.abs(torch.cos(3*x))*(torch.sin(3*x))
y = fx + eps

plt.plot(x,y,label=r"observed data (with error): $(x_i,y_i)$", alpha=0.2)
plt.plot(x,fx,'--',color="C0",label=r"underlying (true, unknown): $e^{-x}|\cos(3x)|\sin(3x)$")
plt.legend()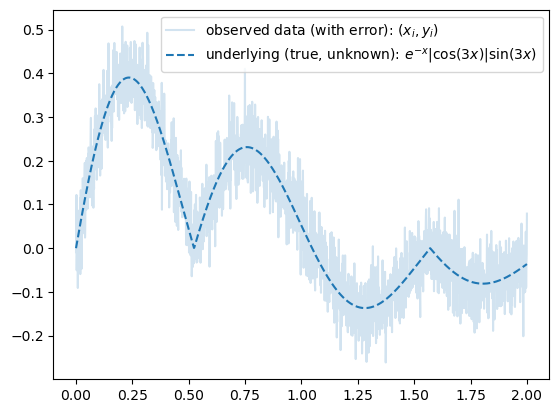

위의 문제는 로지스틱이 아니라 회귀선을 맞춰보는 느낌이 강하기에 MSELoss를 사용

#torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(1,1024),
    torch.nn.ReLU(),
    torch.nn.Linear(1024,1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
#--#
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2
    loss = loss_fn(yhat,y)
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()

plt.plot(x,y,label=r"observed data: $(x_i,y_i)$", alpha=0.2)
plt.plot(x,fx,'--',color="C0",label=r"underlying (true, unkown): $e^{-x}|\cos(3x)|\sin(3x)$")
plt.plot(x,yhat.data,'--',color="C1",label=r"underlying (esimated): $(x_i,\hat{y}_i)$")
plt.legend()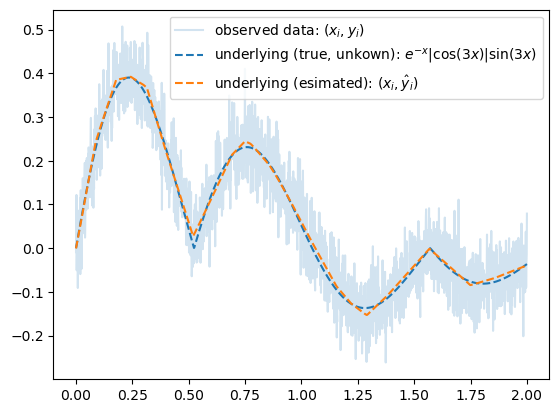

- 이렇게 복잡한 것도 잘 맞춰준다.

11. 그럼 무적인가? (시벤코정리)

치명적인 문제 : Overfiiting

표현력은 무한하지만 오차까지 적합해버리는 문제가 있다

이러한 문제를 해결하기 위해 드랍아웃이라는 기법이 존재함

u = torch.randn(20).reshape(10,2)
u

tensor([[ 0.9303, -1.4108],
        [ 0.1033,  0.3010],
        [-0.3732,  2.3353],
        [ 0.2152,  0.1908],
        [-0.1696,  1.1762],
        [-1.4862, -0.0343],
        [-0.8385,  0.3719],
        [ 0.9422,  0.9081],
        [-1.3018, -0.7977],
        [ 0.1008,  0.2014]])

d = torch.nn.Dropout(0.9)
d(u)

tensor([[ 0.0000, -0.0000],
        [ 1.0332,  0.0000],
        [-0.0000,  0.0000],
        [ 0.0000,  0.0000],
        [-1.6961,  0.0000],
        [-0.0000, -0.0000],
        [-8.3853,  0.0000],
        [ 0.0000,  0.0000],
        [-0.0000, -0.0000],
        [ 0.0000,  2.0141]])

- 드랍아웃

90%의 드랍아웃: 드랍아웃층의 입력 중 임의로 90%를 골라서 결과를 0으로 만든다. + 그리고 0이 되지않고 살아남은 값들은 10배 만큼 값이 커진다.

의미: each iteration (each epoch x) 마다 학습에 참여하는 노드가 랜덤으로 결정됨.

느낌: 모든 노드가 골고루 학습가능 + 한 두개의 특화된 능력치가 개발되기 보다 평균적인 능력치가 전반적으로 개선됨

배깅과 랜덤포레스트의 느낌으로 오버피팅을 해결함