[CD] Dice Problem
Problem 1.
주사위 두 개를 굴려서 나온 눈의 수를 사용해서 두 자리 숫자를 크게 만드는 사람이 이기는 게임이다. 주사위를 처음 굴려서 나온 눈의 수를 10의 자리와 1의 자리 중 어느 곳에 사용할 지 먼저 결정해야 한다. 그런 다음 두 번째로 주사위를 굴려서 나온 눈의 수는 자동으로 남은 자리의 숫자로 사용된다.
예를 들어, 첫 번째 주사위가 3인데 10의 자리로 결정했고, 두 번째 6이 나왔다면 결과는 36이 된다.
어떤 전략을 사용해야 게임에 이길 가능성이 가장 클까?
Data
import pandas as pd
#'https://drive.google.com/file/d/1URY-B3STEDMy38N5PpLyv72QQs0DLykM/view?usp=drive_link'
# 위의 링크에 접속하면 two_dice.csv 파일을 다운받을 수 있습니다.
df = pd.read_csv('two_dice.csv')
df
| dice1 | dice2 | |
|---|---|---|
| 0 | 1 | 4 |
| 1 | 1 | 2 |
| 2 | 5 | 3 |
| 3 | 6 | 2 |
| 4 | 3 | 3 |
| ... | ... | ... |
| 999995 | 3 | 3 |
| 999996 | 2 | 6 |
| 999997 | 4 | 5 |
| 999998 | 3 | 2 |
| 999999 | 2 | 4 |
1000000 rows × 2 columns
Optimal Solution
df['optimal_score'] = df.apply(lambda row: row['dice2'] * 10 + row['dice1']
if row['dice1'] < 4 else row['dice1'] * 10 + row['dice2'], axis=1)
print(f"총점수: {sum(df['optimal_score'])}")
print(f"평균: {sum(df['optimal_score']) / len(df)}")
총점수: 45241257
평균: 45.241257
최적의 방법은 첫 번째 주사위가 1,2,3이 나온다면 1의 자리에 사용하도록 선택하고 4,5,6이 나온다면 10의 자리에 사용하는 것이 최적의 방법이다.
위의 코드는 최적의 방법을 구현한 코드이다.
Graph
import numpy as np
import matplotlib.pyplot as plt
from collections import Counter
x = np.zeros((6, 6), dtype=int)
for dice1 in range(1, 7):
for dice2 in range(1, 7):
if dice1 > 3:
x[dice1 - 1, dice2 - 1] = dice1 * 10 + dice2 # dice1이 4 이상이면 십의 자리로 배치
else:
x[dice1 - 1, dice2 - 1] = dice2 * 10 + dice1 # dice1이 3 이하이면 일의 자리로 배치
values = x.flatten()
count = Counter(values)
prob = {k: v / 36 for k, v in count.items()} # 총 경우의 수 36개
x_values = np.array(list(prob.keys()))
prob_values = np.array(list(prob.values()))
plt.figure(figsize=(10, 5))
plt.bar(x_values, prob_values, color='blue', alpha=0.7)
plt.xlabel("result", fontsize=12)
plt.ylabel("prob", fontsize=12)
plt.title("Distribution of Optimal Scores", fontsize=14)
plt.xticks(rotation=45)
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
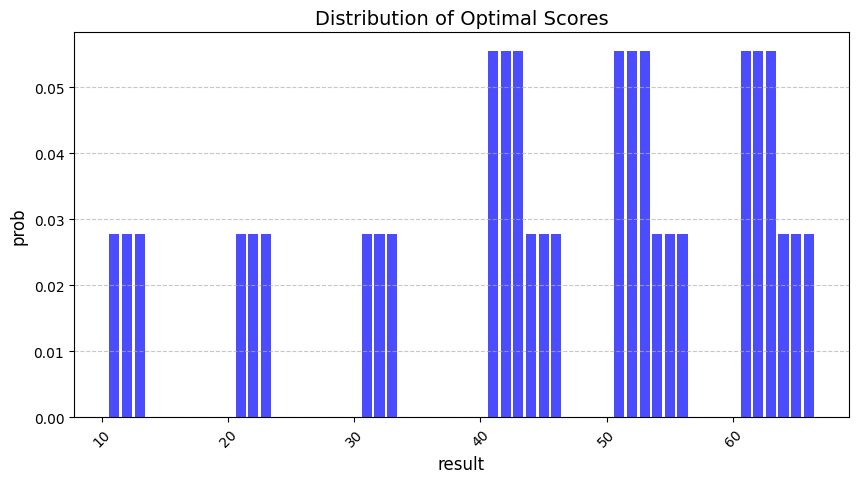
- 최적의 방법을 사용했을 때 어떤 수가 많이 나오는지를 시각화한 것이다. 40 이상의 비교적 큰 수들의 빈도가 많은 것을 보아 최적의 방법이 잘 동작하고 있다는 것을 알 수 있다.
Expectation
import numpy as np
from collections import Counter
# 6x6 행렬을 생성하여 가능한 점수를 저장
x = np.zeros((6, 6), dtype=int)
# 각 주사위 값 조합에 대해 점수 계산
for dice1 in range(1, 7):
for dice2 in range(1, 7):
if dice1 > 3:
x[dice1 - 1, dice2 - 1] = dice1 * 10 + dice2 # dice1이 4 이상이면 십의 자리로 배치
else:
x[dice1 - 1, dice2 - 1] = dice2 * 10 + dice1 # dice1이 3 이하이면 일의 자리로 배치
# 결과값의 확률 계산
values = x.flatten()
count = Counter(values)
prob = {k: v/36 for k, v in count.items()}
# 확률 계산을 위한 결과값 추출
x_values = np.array(list(prob.keys()))
prob_values = np.array(list(prob.values()))
# 기댓값 계산
expected_value = np.sum(x_values * prob_values) # 기댓값 45.25
print("기댓값:", expected_value)
기댓값: 45.25
표본이 충분히 많다면 표본평균은 기댓값(모평균 $μ$)과 매우 유사해진다.
- 하지만 기댓값은 모집단의 평균이므로 표본평균과는 다르다.
Problem 2.
주사위 3개를 굴려서 나온 눈의 수를 사용해서 세자리 숫자를 가장 크게 만드는 사람이 이기는 게임이다.
주사위를 처음 굴려서 나온 눈의 수를 세자리 숫자에서 어느 곳에 사용할 지 먼저 결정한다. 그런 다음 두 번째로 굴린 주사위에서 나온 눈의 수는 남은 두자리의 숫자 중 하나로 결정한다. 세 번째 나온 주사위 눈수는 자동으로 남은 숫자로 사용된다.
예를 들어, 첫 번째 주사위가 3인데 10의 자리로 결정했고, 두 번째 6이 나와 100의 자리 숫자에 사용하고, 세 번째 주사위 눈수가 1이면 결과는 631이 된다.
어떤 전략이 최선의 전략인가?
Data
# https://drive.google.com/file/d/1G_j1AdmgLluS3obeQzf-oABCQYTdSxVL/view?usp=drive_link
# 위의 링크를 접속하면 three_dice.csv를 다운받을 수 있습니다.
df2 = pd.read_csv('three_dice.csv')
df2
| dice1 | dice2 | dice3 | |
|---|---|---|---|
| 0 | 5 | 2 | 4 |
| 1 | 4 | 2 | 3 |
| 2 | 4 | 2 | 5 |
| 3 | 2 | 5 | 4 |
| 4 | 5 | 5 | 5 |
| ... | ... | ... | ... |
| 999995 | 5 | 4 | 4 |
| 999996 | 5 | 1 | 3 |
| 999997 | 4 | 3 | 2 |
| 999998 | 3 | 3 | 6 |
| 999999 | 1 | 6 | 3 |
1000000 rows × 3 columns
Optimal Solution
def get_optimal_score(dice1, dice2, dice3):
positions = {'A': None, 'B': None, 'C': None} # 숫자의 위치를 저장할 딕셔너리
# A: one , B: ten , C: hundred
# 첫 번째 주사위 배치 결정
if dice1 in [1,2]: # 1,2 -> 1의자리 배치
positions['A'] = dice1
elif dice1 in [3,4]: # 3,4 -> 10의 자리 배치
positions['B'] = dice1
else: # 5,6 -> 100의 자리 배치
positions['C'] = dice1
# 두 번째 주사위 배치 결정
remaining_positions = [pos for pos, val in positions.items() if val is None] # 아직 숫자가 배치되지 않은 자리를 리스트로 저장
if dice2 in [1, 2, 3]: # 작은 자리부터 채우기
remaining_positions.sort() # 작은 자리 먼저 (A(one) -> B(ten) 순서)
else: # 큰 자리부터 채우기
remaining_positions.sort(reverse=True) # 큰 자리 먼저 (B(ten) -> A(one) 순서)
positions[remaining_positions[0]] = dice2 # 두 번째 주사위 배치
# 세 번째 주사위는 남은 자리에 배치
remaining_position = [pos for pos, val in positions.items() if val is None][0]
positions[remaining_position] = dice3
# 3자리 숫자 생성
optimal_score = positions['C'] * 100 + positions['B'] * 10 + positions['A']
return optimal_score
# optimal_score 열 추가
df2['optimal_score'] = df2.apply(lambda row: get_optimal_score(row['dice1'], row['dice2'], row['dice3']), axis=1)
print(f"총점수: {df2['optimal_score'].sum()}")
print(f"평균: {df2['optimal_score'].mean()}")
총점수: 503895228
평균: 503.895228
1 최적의 방법은 첫 번째 주사위가 1,2가 나온다면 1의 자리에 사용하도록 선택하고 3,4가 나온다면 10의 자리에 사용, 5,6이 나온다면 100의 자리에 사용한다.
2 그 후 두 번째 주사위의 결과가 1,2,3이라면 남은 자리 중 작은 자리에 사용하고 4,5,6이라면 남은 자리 중 큰 자리에 사용한다.
3 세 번째 주사위는 자동으로 남은 자리에 가게 된다. 이렇게 먼저 번호마다 자리를 정한 후에 3자리 수를 생성해주는 것이 최적의 방법이다.
Graph
import numpy as np
from collections import Counter
# 6x6x6 배열을 생성하여 가능한 점수를 저장
x = np.zeros((6, 6, 6), dtype=int)
# 각 주사위 값 조합에 대해 점수 계산
for dice1 in range(1, 7):
for dice2 in range(1, 7):
for dice3 in range(1, 7):
if dice1 >= 5:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice1 * 100 + dice2 * 10 + dice3
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice1 * 100 + dice3 * 10 + dice2
elif dice1 <= 2:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice2 * 100 + dice3 * 10 + dice1
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice3 * 100 + dice2 * 10 + dice1
else:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice2 * 100 + dice1 * 10 + dice3
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice3 * 100 + dice1 * 10 + dice2
# 결과값의 확률 계산
values = x.flatten()
count = Counter(values)
prob = {k: v / 216 for k, v in count.items()}
# 확률 계산을 위한 결과값 추출
x_values = np.array(list(prob.keys()))
prob_values = np.array(list(prob.values()))
x_values = np.array(list(prob.keys()))
prob_values = np.array(list(prob.values()))
plt.figure(figsize=(10, 5))
plt.bar(x_values, prob_values, color='blue', alpha=0.7)
plt.xlabel("result", fontsize=12)
plt.ylabel("prob", fontsize=12)
plt.title("Distribution of Optimal Scores", fontsize=14)
plt.xticks(rotation=45)
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
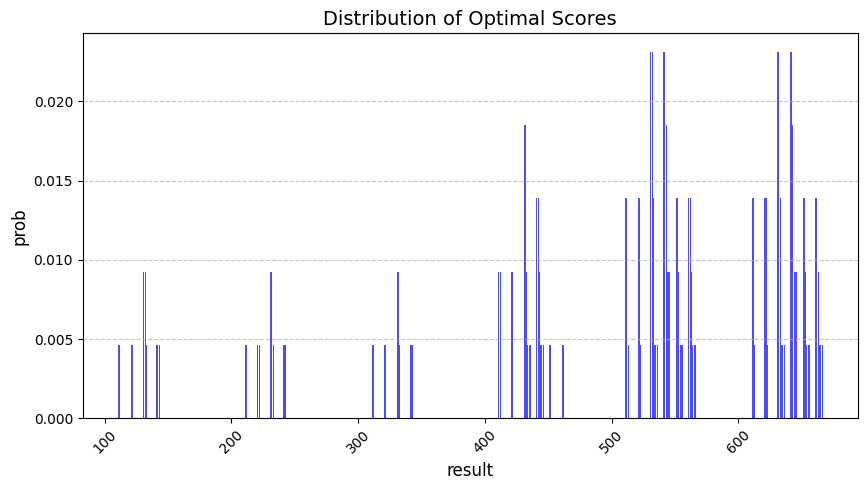
- 최적의 방법을 사용했을 때 어떤 수가 많이 나오는지를 시각화한 것이다. 400 이상의 비교적 큰 수들의 빈도가 많은 것을 보아 최적의 방법이 잘 동작하고 있다는 것을 알 수 있다.
Expectation
import numpy as np
from collections import Counter
# 6x6x6 배열을 생성하여 가능한 점수를 저장
x = np.zeros((6, 6, 6), dtype=int)
# 각 주사위 값 조합에 대해 점수 계산
for dice1 in range(1, 7):
for dice2 in range(1, 7):
for dice3 in range(1, 7):
if dice1 >= 5:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice1 * 100 + dice2 * 10 + dice3
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice1 * 100 + dice3 * 10 + dice2
elif dice1 <= 2:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice2 * 100 + dice3 * 10 + dice1
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice3 * 100 + dice2 * 10 + dice1
else:
if dice2 >= 4:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice2 * 100 + dice1 * 10 + dice3
else:
x[dice1 - 1, dice2 - 1, dice3 - 1] = dice3 * 100 + dice1 * 10 + dice2
# 결과값의 확률 계산
values = x.flatten()
count = Counter(values)
prob = {k: v / 216 for k, v in count.items()}
# 확률 계산을 위한 결과값 추출
x_values = np.array(list(prob.keys()))
prob_values = np.array(list(prob.values()))
# 기댓값 계산
expected_value = np.sum(x_values * prob_values) # 3개의 주사위 기댓값 계산
print("기댓값:", expected_value)
기댓값: 503.99999999999994
표본이 충분히 많다면 표본평균은 기댓값(모평균 $μ$)과 매우 유사해진다.
- 하지만 기댓값은 모집단의 평균이므로 표본평균과는 다르다.